ChapterThree Add LFUCache/LRUCache

leetcode/0146.LRU-Cache/README.md

@@ -55,7 +55,7 @@ lRUCache.get(4);    // return 4
 
 ## 解题思路
 
-- 这一题是 LRU 经典面试题，详细解释见第三章模板。
+- 这一题是 LRU 经典面试题，详细解释见[第三章 LRUCache 模板](https://books.halfrost.com/leetcode/ChapterThree/LRUCache/)。
 
 ## 代码
 

leetcode/0460.LFU-Cache/README.md

@@ -60,7 +60,7 @@ lfu.get(4);      // return 4
 
 ## 解题思路
 
-- 这一题是 LFU 经典面试题，详细解释见第三章模板。
+- 这一题是 LFU 经典面试题，详细解释见[第三章 LFUCache 模板](https://books.halfrost.com/leetcode/ChapterThree/LFUCache/)。
 
 ## 代码
 

website/content/ChapterThree/LFUCache.md

@@ -0,0 +1,360 @@
+---
+title: LFUCache
+type: docs
+---
+
+# 最不经常最少使用 LFUCache
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_1_.png)
+
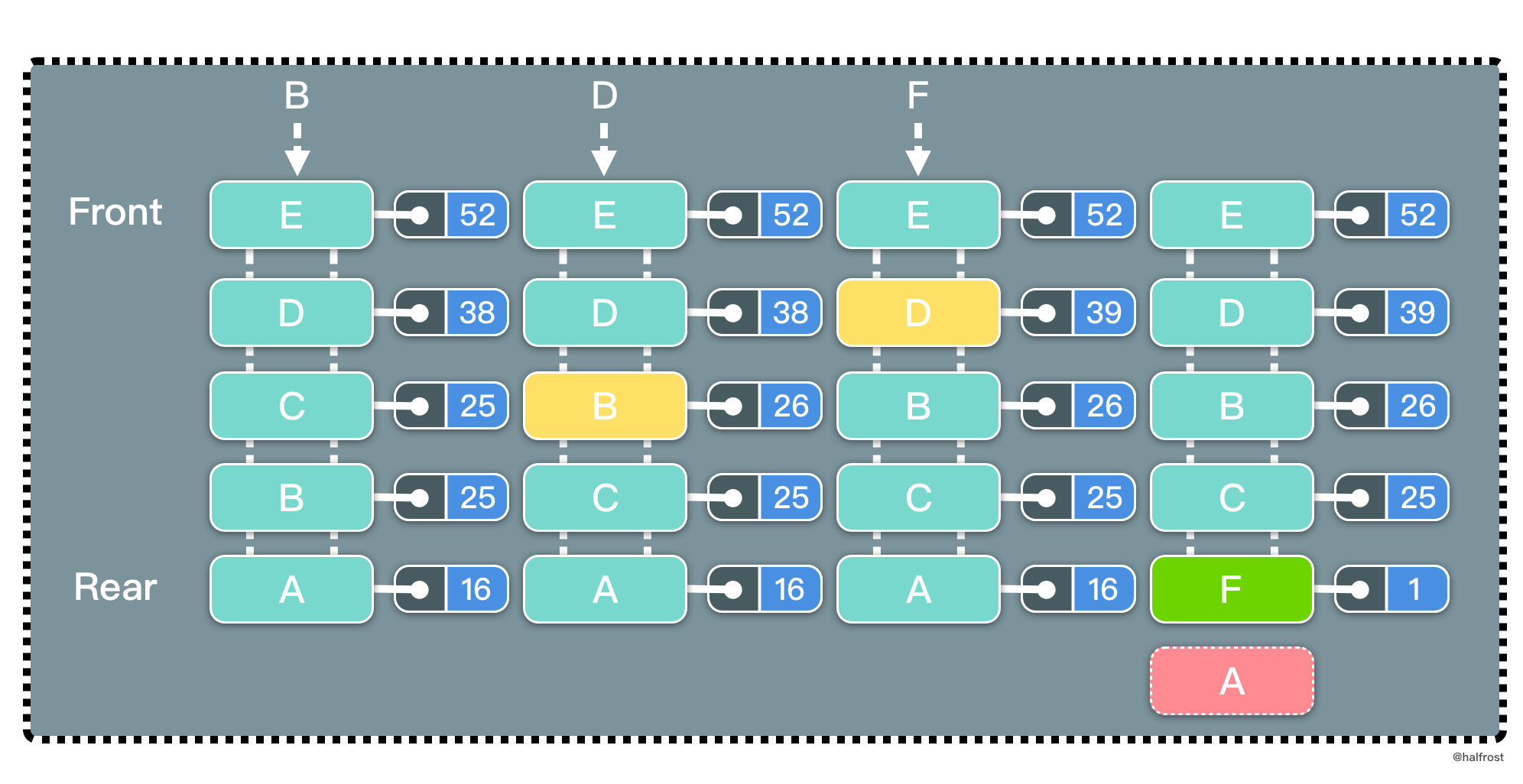
+LFU 是 Least Frequently Used 的缩写，即最不经常最少使用，也是一种常用的页面置换算法，选择访问计数器最小的页面予以淘汰。如下图，缓存中每个页面带一个访问计数器。
+
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_3.png)
+
+根据 LFU 的策略，每访问一次都要更新访问计数器。当插入 B 的时候，发现缓存中有 B，所以增加访问计数器的计数，并把 B 移动到访问计数器从大到小排序的地方。再插入 D，同理先更新计数器，再移动到它排序以后的位置。当插入 F 的时候，缓存中不存在 F，所以淘汰计数器最小的页面的页面，所以淘汰 A 页面。此时 F 排在最下面，计数为 1。
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_8_.png)
+
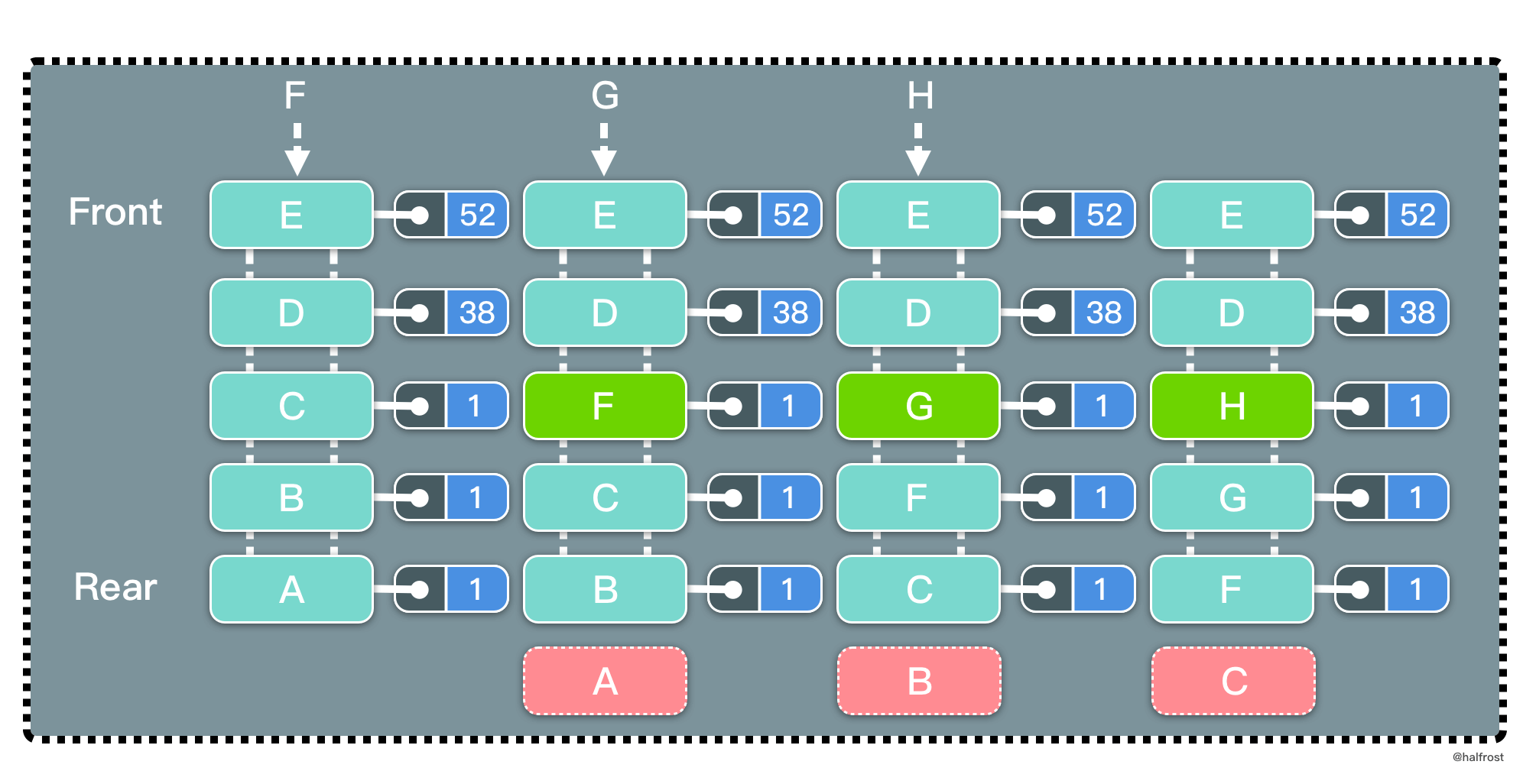
+这里有一个比 LRU 特别的地方。如果淘汰的页面访问次数有多个相同的访问次数，选择最靠尾部的。如上图中，A、B、C 三者的访问次数相同，都是 1 次。要插入 F，F 不在缓存中，此时要淘汰 A 页面。F 是新插入的页面，访问次数为 1，排在 C 的前面。也就是说相同的访问次数，按照新旧顺序排列，淘汰掉最旧的页面。这一点是和 LRU 最大的不同的地方。
+
+可以发现，**LFU 更新和插入新页面可以发生在链表中任意位置，删除页面都发生在表尾**。
+
+
+## 解法一 Get O(1) / Put O(1)
+
+LFU 同样要求查询尽量高效，O(1) 内查询。依旧选用 map 查询。修改和删除也需要 O(1) 完成，依旧选用双向链表，继续复用 container 包中的 list 数据结构。LFU 需要记录访问次数，所以每个结点除了存储 key，value，需要再多存储 frequency 访问次数。
+
+还有 1 个问题需要考虑，一个是如何按频次排序？相同频次，按照先后顺序排序。如果你开始考虑排序算法的话，思考方向就偏离最佳答案了。排序至少 O(nlogn)。重新回看 LFU 的工作原理，会发现它只关心最小频次。其他频次之间的顺序并不关心。所以不需要排序。用一个 min 变量保存最小频次，淘汰时读取这个最小值能找到要删除的结点。相同频次按照先后顺序排列，这个需求还是用双向链表实现，双向链表插入的顺序体现了结点的先后顺序。相同频次对应一个双向链表，可能有多个相同频次，所以可能有多个双向链表。用一个 map 维护访问频次和双向链表的对应关系。删除最小频次时，通过 min 找到最小频次，然后再这个 map 中找到这个频次对应的双向链表，在双向链表中找到最旧的那个结点删除。这就解决了 LFU 删除操作。
+
+LFU 的更新操作和 LRU 类似，也需要用一个 map 保存 key 和双向链表结点的映射关系。这个双向链表结点中存储的是 key-value-frequency 三个元素的元组。这样通过结点中的 key 和 frequency 可以反过来删除 map 中的 key。
+
+定义 LFUCache 的数据结构如下：
+
+```go
+
+import "container/list"
+
+type LFUCache struct {
+	nodes    map[int]*list.Element
+	lists    map[int]*list.List
+	capacity int
+	min      int
+}
+
+type node struct {
+	key       int
+	value     int
+	frequency int
+}
+
+func Constructor(capacity int) LFUCache {
+	return LFUCache{nodes: make(map[int]*list.Element),
+		lists:    make(map[int]*list.List),
+		capacity: capacity,
+		min:      0,
+	}
+}
+
+```
+
+LFUCache 的 Get 操作涉及更新 frequency 值和 2 个 map。在 nodes map 中通过 key 获取到结点信息。在 lists 删除结点当前 frequency 结点。删完以后 frequency ++。新的 frequency 如果在 lists 中存在，添加到双向链表表首，如果不存在，需要新建一个双向链表并把当前结点加到表首。再更新双向链表结点作为 value 的 map。最后更新 min 值，判断老的 frequency 对应的双向链表中是否已经为空，如果空了，min++。
+
+```go
+func (this *LFUCache) Get(key int) int {
+	value, ok := this.nodes[key]
+	if !ok {
+		return -1
+	}
+	currentNode := value.Value.(*node)
+	this.lists[currentNode.frequency].Remove(value)
+	currentNode.frequency++
+	if _, ok := this.lists[currentNode.frequency]; !ok {
+		this.lists[currentNode.frequency] = list.New()
+	}
+	newList := this.lists[currentNode.frequency]
+	newNode := newList.PushFront(currentNode)
+	this.nodes[key] = newNode
+	if currentNode.frequency-1 == this.min && this.lists[currentNode.frequency-1].Len() == 0 {
+		this.min++
+	}
+	return currentNode.value
+}
+
+```
+
+LFU 的 Put 操作逻辑稍微多一点。先在 nodes map 中查询 key 是否存在，如果存在，获取这个结点，更新它的 value 值，然后手动调用一次 Get 操作，因为下面的更新逻辑和 Get 操作一致。如果 map 中不存在，接下来进行插入或者删除操作。判断 capacity 是否装满，如果装满，执行删除操作。在 min 对应的双向链表中删除表尾的结点，对应的也要删除 nodes map 中的键值。
+
+由于新插入的页面访问次数一定为 1，所以 min 此时置为 1。新建结点，插入到 2 个 map 中。
+
+```go
+
+func (this *LFUCache) Put(key int, value int) {
+	if this.capacity == 0 {
+		return
+	}
+	// 如果存在，更新访问次数
+	if currentValue, ok := this.nodes[key]; ok {
+		currentNode := currentValue.Value.(*node)
+		currentNode.value = value
+		this.Get(key)
+		return
+	}
+	// 如果不存在且缓存满了，需要删除
+	if this.capacity == len(this.nodes) {
+		currentList := this.lists[this.min]
+		backNode := currentList.Back()
+		delete(this.nodes, backNode.Value.(*node).key)
+		currentList.Remove(backNode)
+	}
+	// 新建结点，插入到 2 个 map 中
+	this.min = 1
+	currentNode := &node{
+		key:       key,
+		value:     value,
+		frequency: 1,
+	}
+	if _, ok := this.lists[1]; !ok {
+		this.lists[1] = list.New()
+	}
+	newList := this.lists[1]
+	newNode := newList.PushFront(currentNode)
+	this.nodes[key] = newNode
+}
+
+```
+
+总结，LFU 是由两个 map 和一个 min 指针组成的数据结构。一个 map 中 key 存的是访问次数，对应的 value 是一个个的双向链表，此处双向链表的作用是在相同频次的情况下，淘汰表尾最旧的那个页面。另一个 map 中 key 对应的 value 是双向链表的结点，结点中比 LRU 多存储了一个访问次数的值，即结点中存储 key-value-frequency 的元组。此处双向链表的作用和 LRU 是类似的，可以根据 map 中的 key 更新双向链表结点中的 value 和 frequency 的值，也可以根据双向链表结点中的 key 和 frequency 反向更新 map 中的对应关系。如下图：
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_10_0.png)
+
+提交代码以后，成功通过所有测试用例。
+
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_5.png)
+
+
+## 解法二 Get O(capacity) / Put O(capacity)
+
+LFU 的另外一个思路是利用 [Index Priority Queue](https://algs4.cs.princeton.edu/24pq/) 这个数据结构。别被名字吓到，Index Priority Queue = map + Priority Queue，仅此而已。
+
+利用 Priority Queue 维护一个最小堆，堆顶是访问次数最小的元素。map 中的 value 存储的是优先队列中结点。
+
+```go
+import "container/heap"
+
+type LFUCache struct {
+	capacity int
+	pq       PriorityQueue
+	hash     map[int]*Item
+	counter  int
+}
+
+func Constructor(capacity int) LFUCache {
+	lfu := LFUCache{
+		pq:       PriorityQueue{},
+		hash:     make(map[int]*Item, capacity),
+		capacity: capacity,
+	}
+	return lfu
+}
+
+```
+
+Get 和 Put 操作要尽量的快，有 2 个问题需要解决。当访问次数相同时，如何删除掉最久的元素？当元素的访问次数发生变化时，如何快速调整堆？为了解决这 2 个问题，定义如下的数据结构：
+
+```go
+// An Item is something we manage in a priority queue.
+type Item struct {
+	value     int // The value of the item; arbitrary.
+	key       int
+	frequency int // The priority of the item in the queue.
+	count     int // use for evicting the oldest element
+	// The index is needed by update and is maintained by the heap.Interface methods.
+	index int // The index of the item in the heap.
+}
+
+```
+
+堆中的结点存储这 5 个值。count 值用来决定哪个是最老的元素，类似一个操作时间戳。index 值用来 re-heapify 调整堆的。接下来实现 PriorityQueue 的方法。
+
+```go
+// A PriorityQueue implements heap.Interface and holds Items.
+type PriorityQueue []*Item
+
+func (pq PriorityQueue) Len() int { return len(pq) }
+
+func (pq PriorityQueue) Less(i, j int) bool {
+	// We want Pop to give us the highest, not lowest, priority so we use greater than here.
+	if pq[i].frequency == pq[j].frequency {
+		return pq[i].count < pq[j].count
+	}
+	return pq[i].frequency < pq[j].frequency
+}
+
+func (pq PriorityQueue) Swap(i, j int) {
+	pq[i], pq[j] = pq[j], pq[i]
+	pq[i].index = i
+	pq[j].index = j
+}
+
+func (pq *PriorityQueue) Push(x interface{}) {
+	n := len(*pq)
+	item := x.(*Item)
+	item.index = n
+	*pq = append(*pq, item)
+}
+
+func (pq *PriorityQueue) Pop() interface{} {
+	old := *pq
+	n := len(old)
+	item := old[n-1]
+	old[n-1] = nil  // avoid memory leak
+	item.index = -1 // for safety
+	*pq = old[0 : n-1]
+	return item
+}
+
+// update modifies the priority and value of an Item in the queue.
+func (pq *PriorityQueue) update(item *Item, value int, frequency int, count int) {
+	item.value = value
+	item.count = count
+	item.frequency = frequency
+	heap.Fix(pq, item.index)
+}
+```
+
+在 Less() 方法中，frequency 从小到大排序，frequency 相同的，按 count 从小到大排序。按照优先队列建堆规则，可以得到，frequency 最小的在堆顶，相同的 frequency，count 最小的越靠近堆顶。
+
+在 Swap() 方法中，记得要更新 index 值。在 Push() 方法中，插入时队列的长度即是该元素的 index 值，此处也要记得更新 index 值。update() 方法调用 Fix() 函数。Fix() 函数比先 Remove() 再 Push() 一个新的值，花销要小。所以此处调用 Fix() 函数，这个操作的时间复杂度是 O(log n)。
+
+这样就维护了最小 Index Priority Queue。Get 操作非常简单：
+
+```go
+func (this *LFUCache) Get(key int) int {
+	if this.capacity == 0 {
+		return -1
+	}
+	if item, ok := this.hash[key]; ok {
+		this.counter++
+		this.pq.update(item, item.value, item.frequency+1, this.counter)
+		return item.value
+	}
+	return -1
+}
+
+```
+
+在 hashmap 中查询 key，如果存在，counter 时间戳累加，调用 Priority Queue 的 update 方法，调整堆。
+
+```go
+func (this *LFUCache) Put(key int, value int) {
+	if this.capacity == 0 {
+		return
+	}
+	this.counter++
+	// 如果存在，增加 frequency，再调整堆
+	if item, ok := this.hash[key]; ok {
+		this.pq.update(item, value, item.frequency+1, this.counter)
+		return
+	}
+	// 如果不存在且缓存满了，需要删除。在 hashmap 和 pq 中删除。
+	if len(this.pq) == this.capacity {
+		item := heap.Pop(&this.pq).(*Item)
+		delete(this.hash, item.key)
+	}
+	// 新建结点，在 hashmap 和 pq 中添加。
+	item := &Item{
+		value: value,
+		key:   key,
+		count: this.counter,
+	}
+	heap.Push(&this.pq, item)
+	this.hash[key] = item
+}
+```
+
+
+用最小堆实现的 LFU，Put 时间复杂度是 O(capacity)，Get 时间复杂度是 O(capacity)，不及 2 个 map 实现的版本。巧的是最小堆的版本居然打败了 100%。
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_7.png)
+
+
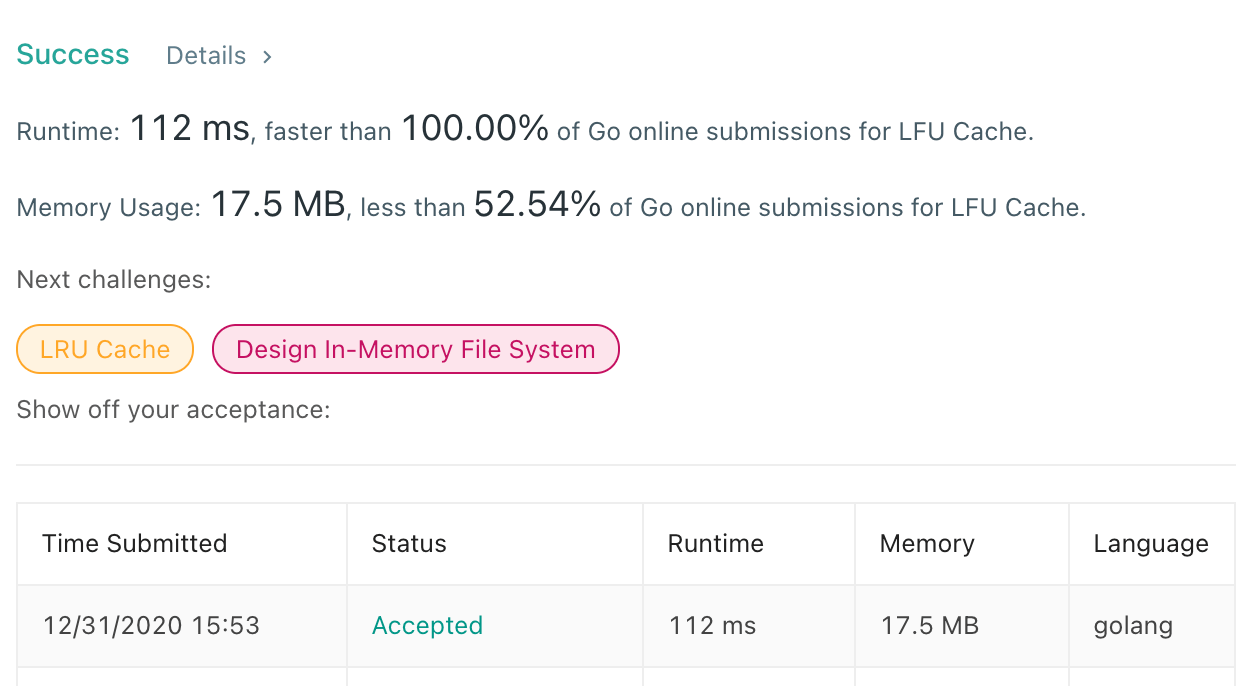
+## 模板
+
+
+```go
+import "container/list"
+
+type LFUCache struct {
+	nodes    map[int]*list.Element
+	lists    map[int]*list.List
+	capacity int
+	min      int
+}
+
+type node struct {
+	key       int
+	value     int
+	frequency int
+}
+
+func Constructor(capacity int) LFUCache {
+	return LFUCache{nodes: make(map[int]*list.Element),
+		lists:    make(map[int]*list.List),
+		capacity: capacity,
+		min:      0,
+	}
+}
+
+func (this *LFUCache) Get(key int) int {
+	value, ok := this.nodes[key]
+	if !ok {
+		return -1
+	}
+	currentNode := value.Value.(*node)
+	this.lists[currentNode.frequency].Remove(value)
+	currentNode.frequency++
+	if _, ok := this.lists[currentNode.frequency]; !ok {
+		this.lists[currentNode.frequency] = list.New()
+	}
+	newList := this.lists[currentNode.frequency]
+	newNode := newList.PushBack(currentNode)
+	this.nodes[key] = newNode
+	if currentNode.frequency-1 == this.min && this.lists[currentNode.frequency-1].Len() == 0 {
+		this.min++
+	}
+	return currentNode.value
+}
+
+func (this *LFUCache) Put(key int, value int) {
+	if this.capacity == 0 {
+		return
+	}
+	if currentValue, ok := this.nodes[key]; ok {
+		currentNode := currentValue.Value.(*node)
+		currentNode.value = value
+		this.Get(key)
+		return
+	}
+	if this.capacity == len(this.nodes) {
+		currentList := this.lists[this.min]
+		frontNode := currentList.Front()
+		delete(this.nodes, frontNode.Value.(*node).key)
+		currentList.Remove(frontNode)
+	}
+	this.min = 1
+	currentNode := &node{
+		key:       key,
+		value:     value,
+		frequency: 1,
+	}
+	if _, ok := this.lists[1]; !ok {
+		this.lists[1] = list.New()
+	}
+	newList := this.lists[1]
+	newNode := newList.PushBack(currentNode)
+	this.nodes[key] = newNode
+}
+
+```

website/content/ChapterThree/LRUCache.md

@@ -0,0 +1,272 @@
+---
+title: LRUCache
+type: docs
+---
+
+# 最近最少使用 LRUCache
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_1_.png)
+
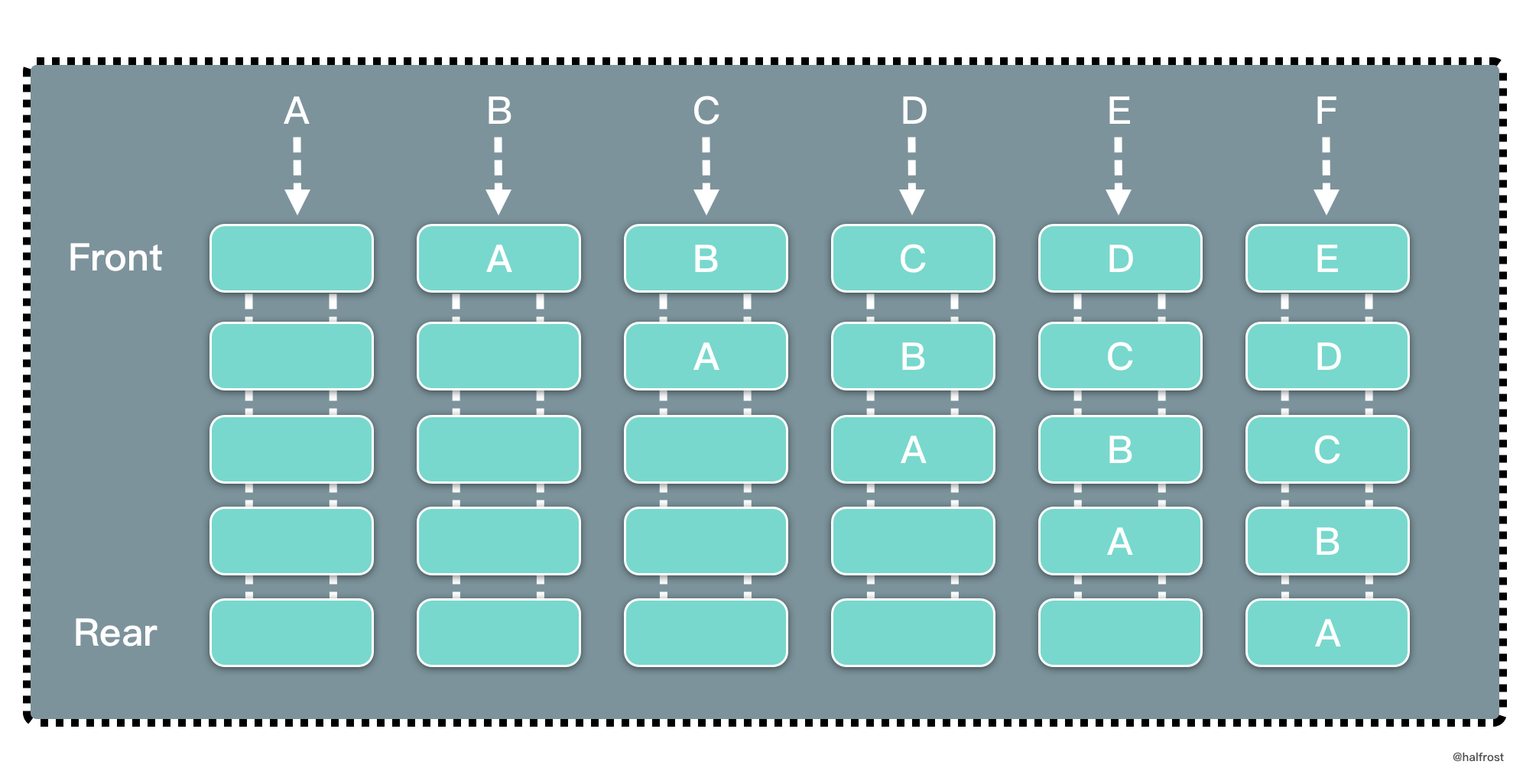
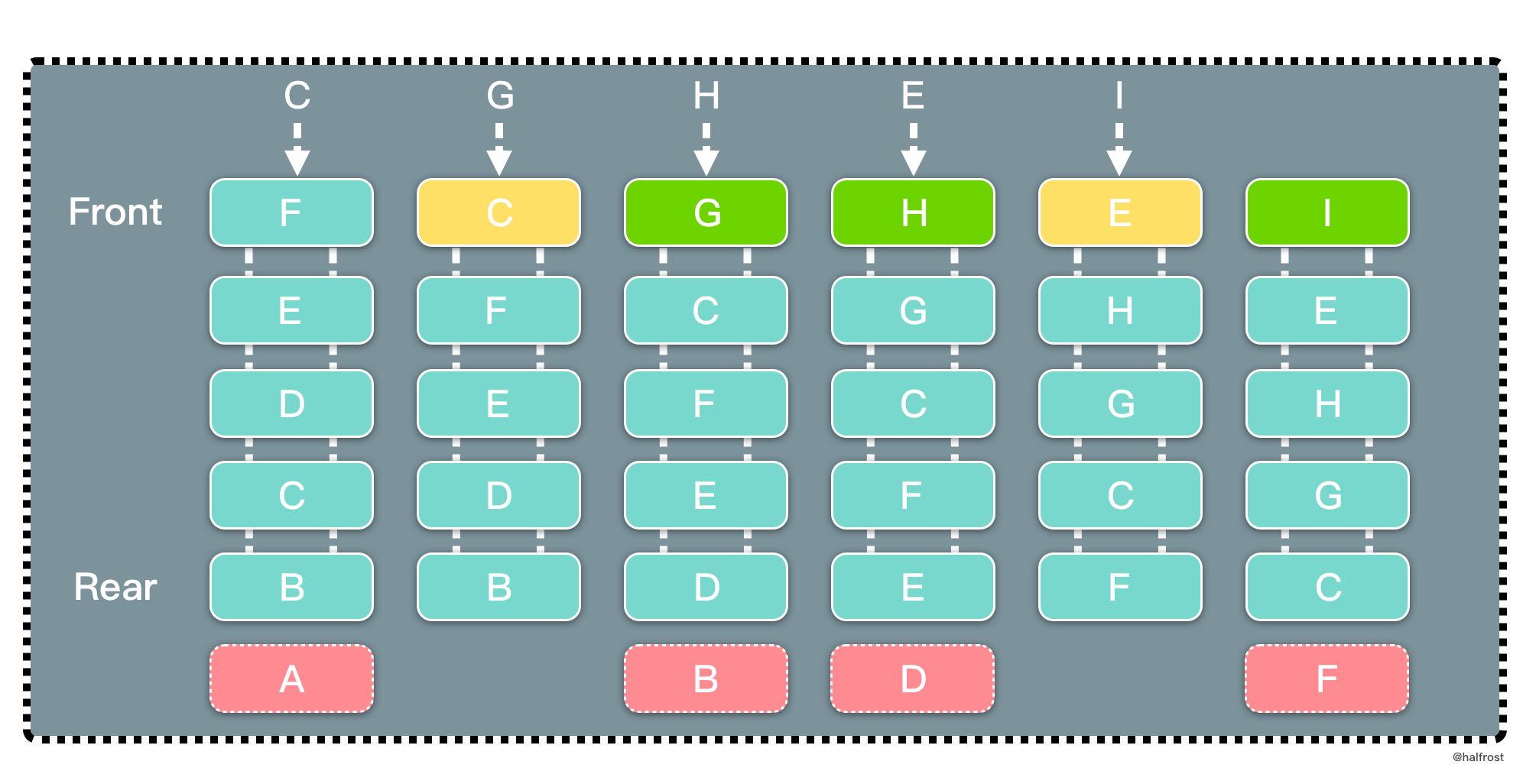
+LRU 是 Least Recently Used 的缩写，即最近最少使用，是一种常用的页面置换算法，选择最近最久未使用的页面予以淘汰。如上图，要插入 F 的时候，此时需要淘汰掉原来的一个页面。
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_2_0.png)
+
+根据 LRU 的策略，每次都淘汰最近最久未使用的页面，所以先淘汰 A 页面。再插入 C 的时候，发现缓存中有 C 页面，这个时候需要把 C 页面放到首位，因为它被使用了。以此类推，插入 G 页面，G 页面是新页面，不在缓存中，所以淘汰掉 B 页面。插入 H 页面，H 页面是新页面，不在缓存中，所以淘汰掉 D 页面。插入 E 的时候，发现缓存中有 E 页面，这个时候需要把 E 页面放到首位。插入 I 页面，I 页面是新页面，不在缓存中，所以淘汰掉 F 页面。
+
+可以发现，**LRU 更新和插入新页面都发生在链表首，删除页面都发生在链表尾**。
+
+## 解法一 Get O(1) / Put O(1)
+
+LRU 要求查询尽量高效，O(1) 内查询。那肯定选用 map 查询。修改，删除也要尽量 O(1) 完成。搜寻常见的数据结构，链表，栈，队列，树，图。树和图排除，栈和队列无法任意查询中间的元素，也排除。所以选用链表来实现。但是如果选用单链表，删除这个结点，需要 O(n) 遍历一遍找到前驱结点。所以选用双向链表，在删除的时候也能 O(1) 完成。
+
+由于 Go 的 container 包中的 list 底层实现是双向链表，所以可以直接复用这个数据结构。定义 LRUCache 的数据结构如下：
+
+```go
+import "container/list"
+
+type LRUCache struct {
+    Cap  int
+    Keys map[int]*list.Element
+    List *list.List
+}
+
+type pair struct {
+    K, V int
+}
+
+func Constructor(capacity int) LRUCache {
+    return LRUCache{
+        Cap: capacity,
+        Keys: make(map[int]*list.Element),
+        List: list.New(),
+    }
+}
+
+```
+
+这里需要解释 2 个问题，list 中的值存的是什么？pair 这个结构体有什么用？
+
+```go
+type Element struct {
+	// Next and previous pointers in the doubly-linked list of elements.
+	// To simplify the implementation, internally a list l is implemented
+	// as a ring, such that &l.root is both the next element of the last
+	// list element (l.Back()) and the previous element of the first list
+	// element (l.Front()).
+	next, prev *Element
+
+	// The list to which this element belongs.
+	list *List
+
+	// The value stored with this element.
+	Value interface{}
+}
+```
+
+在 container/list 中，这个双向链表的每个结点的类型是 Element。Element 中存了 4 个值，前驱和后继结点，双向链表的头结点，value 值。这里的 value 是 interface 类型。笔者在这个 value 里面存了 pair 这个结构体。这就解释了 list 里面存的是什么数据。
+
+为什么要存 pair 呢？单单指存 v 不行么，为什么还要存一份 key ？原因是在 LRUCache 执行删除操作的时候，需要维护 2 个数据结构，一个是 map，一个是双向链表。在双向链表中删除淘汰出去的 value，在 map 中删除淘汰出去 value 对应的 key。如果在双向链表的 value 中不存储 key，那么再删除 map 中的 key 的时候有点麻烦。如果硬要实现，需要先获取到双向链表这个结点 Element 的地址。然后遍历 map，在 map 中找到存有这个 Element 元素地址对应的 key，再删除。这样做时间复杂度是 O(n)，做不到 O(1)。所以双向链表中的 Value 需要存储这个 pair。
+
+LRUCache 的 Get 操作很简单，在 map 中直接读取双向链表的结点。如果 map 中存在，将它移动到双向链表的表头，并返回它的 value 值，如果 map 中不存在，返回 -1。
+
+```go 
+func (c *LRUCache) Get(key int) int {
+	if el, ok := c.Keys[key]; ok {
+		c.List.MoveToFront(el)
+		return el.Value.(pair).V
+	}
+	return -1
+}
+```
+
+LRUCache 的 Put 操作也不难。先查询 map 中是否存在 key，如果存在，更新它的 value，并且把该结点移到双向链表的表头。如果 map 中不存在，新建这个结点加入到双向链表和 map 中。最后别忘记还需要维护双向链表的 cap，如果超过 cap，需要淘汰最后一个结点，双向链表中删除这个结点，map 中删掉这个结点对应的 key。
+
+```go
+func (c *LRUCache) Put(key int, value int) {
+	if el, ok := c.Keys[key]; ok {
+		el.Value = pair{K: key, V: value}
+		c.List.MoveToFront(el)
+	} else {
+		el := c.List.PushFront(pair{K: key, V: value})
+		c.Keys[key] = el
+	}
+	if c.List.Len() > c.Cap {
+		el := c.List.Back()
+		c.List.Remove(el)
+		delete(c.Keys, el.Value.(pair).K)
+	}
+}
+
+```
+
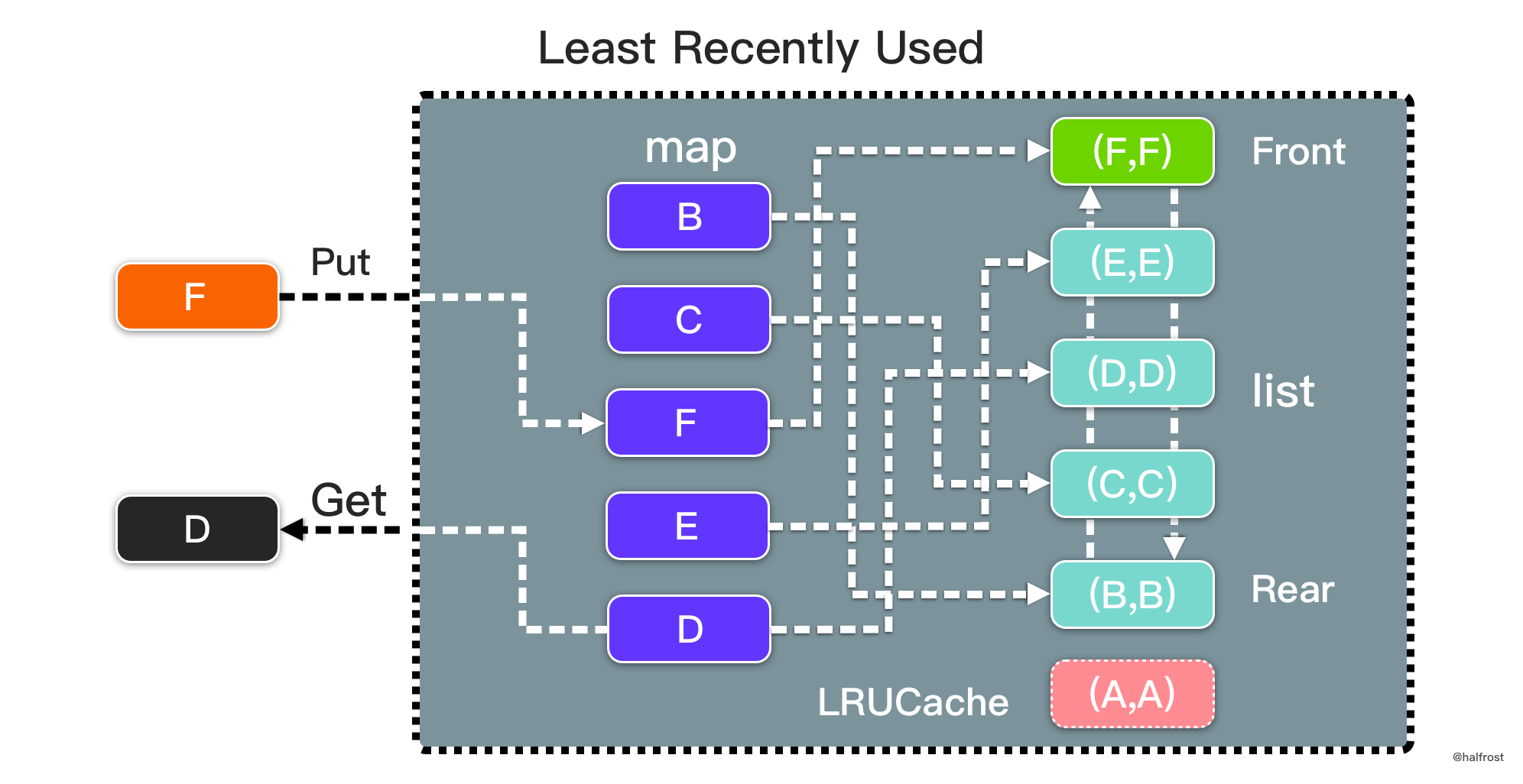
+总结，LRU 是由一个 map 和一个双向链表组成的数据结构。map 中 key 对应的 value 是双向链表的结点。双向链表中存储 key-value 的 pair。双向链表表首更新缓存，表尾淘汰缓存。如下图：
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_9.png)
+
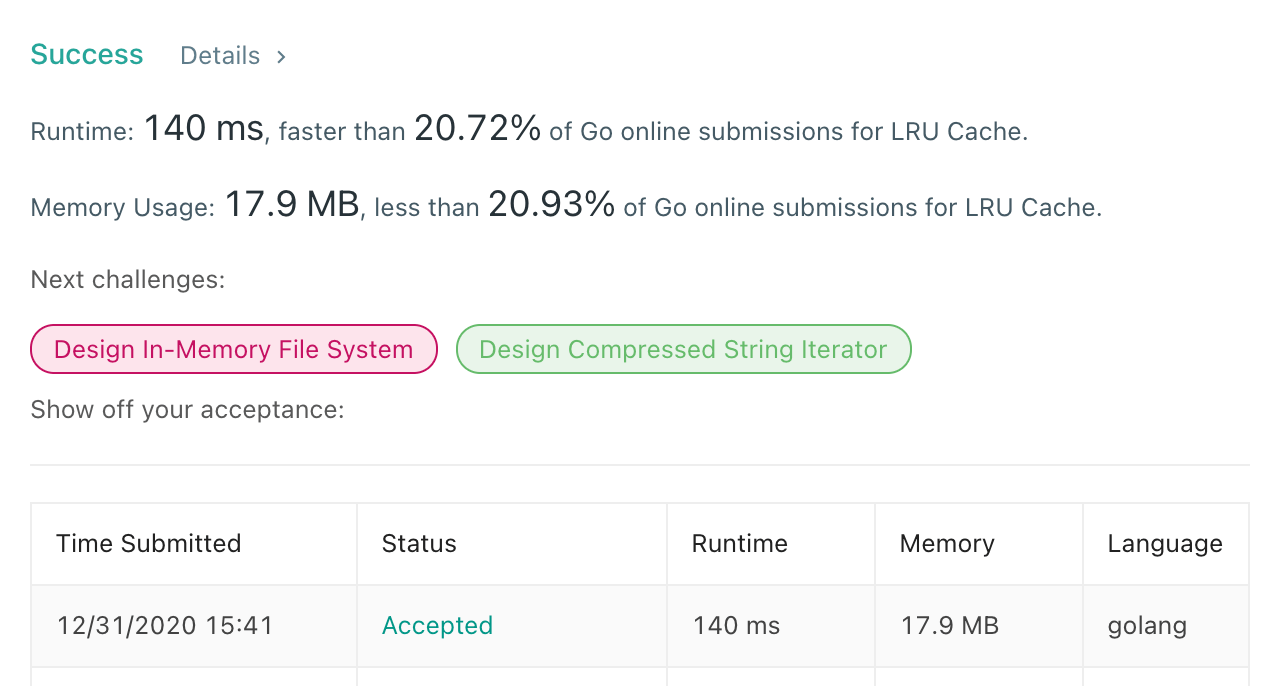
+提交代码以后，成功通过所有测试用例。
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_4_.png)
+
+
+## 解法二 Get O(1) / Put O(1)
+
+数据结构上想不到其他解法了，但从打败的百分比上，看似还有常数的优化空间。笔者反复思考，觉得可能导致运行时间变长的地方是在 interface{} 类型推断，其他地方已无优化的空间。手写一个双向链表提交试试，代码如下：
+
+```go
+
+type LRUCache struct {
+	head, tail *Node
+	keys       map[int]*Node
+	capacity   int
+}
+
+type Node struct {
+	key, val   int
+	prev, next *Node
+}
+
+func ConstructorLRU(capacity int) LRUCache {
+	return LRUCache{keys: make(map[int]*Node), capacity: capacity}
+}
+
+func (this *LRUCache) Get(key int) int {
+	if node, ok := this.keys[key]; ok {
+		this.Remove(node)
+		this.Add(node)
+		return node.val
+	}
+	return -1
+}
+
+func (this *LRUCache) Put(key int, value int) {
+	if node, ok := this.keys[key]; ok {
+		node.val = value
+		this.Remove(node)
+		this.Add(node)
+		return
+	} else {
+		node = &Node{key: key, val: value}
+		this.keys[key] = node
+		this.Add(node)
+	}
+	if len(this.keys) > this.capacity {
+		delete(this.keys, this.tail.key)
+		this.Remove(this.tail)
+	}
+}
+
+func (this *LRUCache) Add(node *Node) {
+	node.prev = nil
+	node.next = this.head
+	if this.head != nil {
+		this.head.prev = node
+	}
+	this.head = node
+	if this.tail == nil {
+		this.tail = node
+		this.tail.next = nil
+	}
+}
+
+func (this *LRUCache) Remove(node *Node) {
+	if node == this.head {
+		this.head = node.next
+		if node.next != nil {
+			node.next.prev = nil
+		}
+		node.next = nil
+		return
+	}
+	if node == this.tail {
+		this.tail = node.prev
+		node.prev.next = nil
+		node.prev = nil
+		return
+	}
+	node.prev.next = node.next
+	node.next.prev = node.prev
+}
+
+```
+
+提交以后还真的 100% 了。
+
+![](https://img.halfrost.com/Blog/ArticleImage/146_6.png)
+
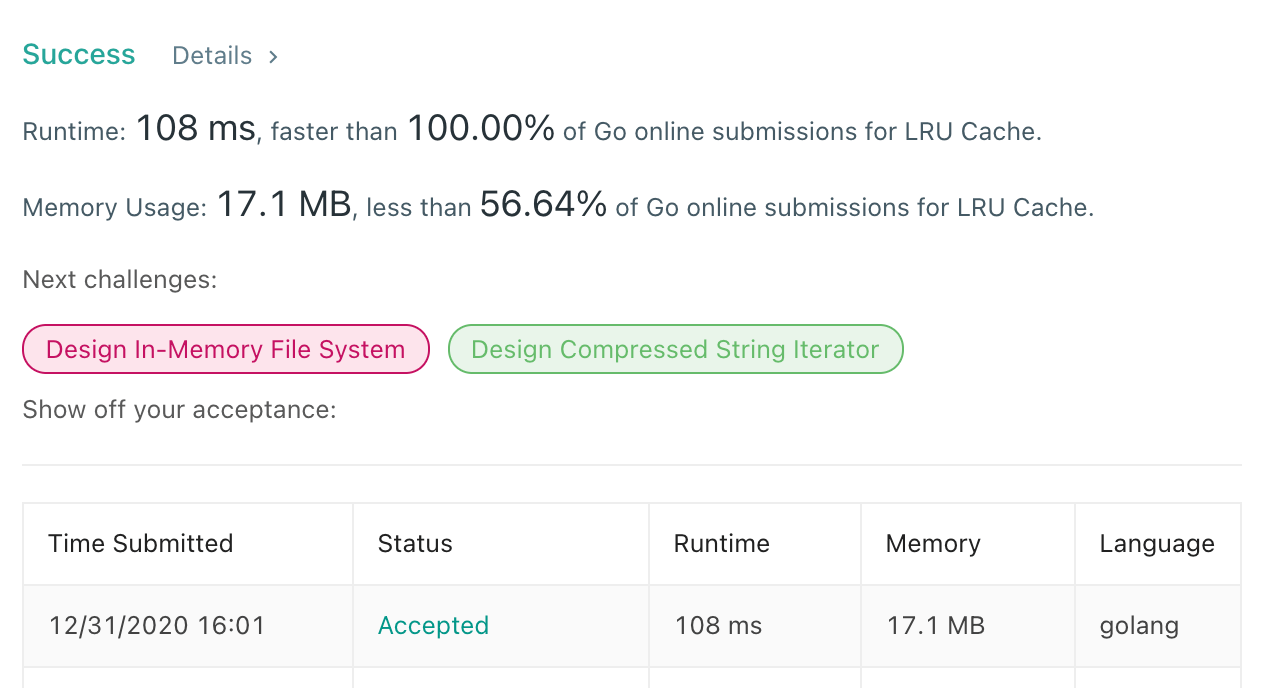
+上述代码实现的 LRU 本质并没有优化，只是换了一个写法，没有用 container 包而已。
+
+
+## 模板
+
+```go
+type LRUCache struct {
+	head, tail *Node
+	Keys       map[int]*Node
+	Cap        int
+}
+
+type Node struct {
+	Key, Val   int
+	Prev, Next *Node
+}
+
+func Constructor(capacity int) LRUCache {
+	return LRUCache{Keys: make(map[int]*Node), Cap: capacity}
+}
+
+func (this *LRUCache) Get(key int) int {
+	if node, ok := this.Keys[key]; ok {
+		this.Remove(node)
+		this.Add(node)
+		return node.Val
+	}
+	return -1
+}
+
+func (this *LRUCache) Put(key int, value int) {
+	if node, ok := this.Keys[key]; ok {
+		node.Val = value
+		this.Remove(node)
+		this.Add(node)
+		return
+	} else {
+		node = &Node{Key: key, Val: value}
+		this.Keys[key] = node
+		this.Add(node)
+	}
+	if len(this.Keys) > this.Cap {
+		delete(this.Keys, this.tail.Key)
+		this.Remove(this.tail)
+	}
+}
+
+func (this *LRUCache) Add(node *Node) {
+	node.Prev = nil
+	node.Next = this.head
+	if this.head != nil {
+		this.head.Prev = node
+	}
+	this.head = node
+	if this.tail == nil {
+		this.tail = node
+		this.tail.Next = nil
+	}
+}
+
+func (this *LRUCache) Remove(node *Node) {
+	if node == this.head {
+		this.head = node.Next
+		node.Next = nil
+		return
+	}
+	if node == this.tail {
+		this.tail = node.Prev
+		node.Prev.Next = nil
+		node.Prev = nil
+		return
+	}
+	node.Prev.Next = node.Next
+	node.Next.Prev = node.Prev
+}
+
+```

website/content/menu/index.md

@@ -31,6 +31,8 @@ headless: true
 - [第三章 一些模板]({{< relref "/ChapterThree/_index.md" >}})
   - [3.1 Segment Tree]({{< relref "/ChapterThree/Segment_Tree.md" >}})
   - [3.2 UnionFind]({{< relref "/ChapterThree/UnionFind.md" >}})
+  - [3.3 LRUCache]({{< relref "/ChapterThree/LRUCache.md" >}})
+  - [3.4 LFUCache]({{< relref "/ChapterThree/LFUCache.md" >}})
 - [第四章 Leetcode 题解]({{< relref "/ChapterFour/_index.md" >}})
     - [0001.Two-Sum]({{< relref "/ChapterFour/0001.Two-Sum.md" >}})
     - [0002.Add-Two-Numbers]({{< relref "/ChapterFour/0002.Add-Two-Numbers.md" >}})