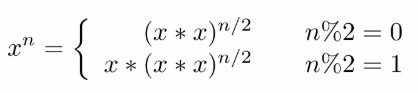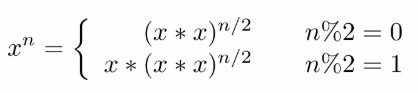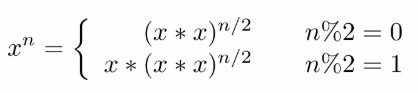diff --git a/docs/notes/16. 数值的整数次方.md b/docs/notes/16. 数值的整数次方.md
index 1cddc018..e8e579fc 100644
--- a/docs/notes/16. 数值的整数次方.md
+++ b/docs/notes/16. 数值的整数次方.md
@@ -1,37 +1,46 @@
# 16. 数值的整数次方
-[NowCoder](https://www.nowcoder.com/practice/1a834e5e3e1a4b7ba251417554e07c00?tpId=13&tqId=11165&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking&from=cyc_github)
+## 题目链接
+
+[牛客网](https://www.nowcoder.com/practice/1a834e5e3e1a4b7ba251417554e07c00?tpId=13&tqId=11165&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking&from=cyc_github)
## 题目描述
-给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
+给定一个 double 类型的浮点数 x和 int 类型的整数 n,求 x 的 n 次方。
## 解题思路
-下面的讨论中 x 代表 base,n 代表 exponent。
+
-
+最直观的解法是将 x 重复乘 n 次,x\*x\*x...\*x,那么时间复杂度为 O(N)。因为乘法是可交换的,所以可以将上述操作拆开成两半 (x\*x..\*x)\* (x\*x..\*x),两半的计算是一样的,因此只需要计算一次。而且对于新拆开的计算,又可以继续拆开。这就是分治思想,将原问题的规模拆成多个规模较小的子问题,最后子问题的解合并起来。
-
+本题中子问题是 xn/2,在将子问题合并时将子问题的解乘于自身相乘即可。但如果 n 不为偶数,那么拆成两半还会剩下一个 x,在将子问题合并时还需要需要多乘于一个 x。
+
+
+
+
因为 (x\*x)n/2 可以通过递归求解,并且每次递归 n 都减小一半,因此整个算法的时间复杂度为 O(logN)。
```java
-public double Power(double base, int exponent) {
- if (exponent == 0)
- return 1;
- if (exponent == 1)
- return base;
+public double Power(double x, int n) {
boolean isNegative = false;
- if (exponent < 0) {
- exponent = -exponent;
+ if (n < 0) {
+ n = -n;
isNegative = true;
}
- double pow = Power(base * base, exponent / 2);
- if (exponent % 2 != 0)
- pow = pow * base;
- return isNegative ? 1 / pow : pow;
+ double res = pow(x, n);
+ return isNegative ? 1 / res : res;
+}
+
+private double pow(double x, int n) {
+ if (n == 0) return 1;
+ if (n == 1) return x;
+ double res = pow(x, n / 2);
+ res = res * res;
+ if (n % 2 != 0) res *= x;
+ return res;
}
```
@@ -40,4 +49,5 @@ public double Power(double base, int exponent) {
+
diff --git a/notes/16. 数值的整数次方.md b/notes/16. 数值的整数次方.md
index 1cddc018..e8e579fc 100644
--- a/notes/16. 数值的整数次方.md
+++ b/notes/16. 数值的整数次方.md
@@ -1,37 +1,46 @@
# 16. 数值的整数次方
-[NowCoder](https://www.nowcoder.com/practice/1a834e5e3e1a4b7ba251417554e07c00?tpId=13&tqId=11165&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking&from=cyc_github)
+## 题目链接
+
+[牛客网](https://www.nowcoder.com/practice/1a834e5e3e1a4b7ba251417554e07c00?tpId=13&tqId=11165&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking&from=cyc_github)
## 题目描述
-给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
+给定一个 double 类型的浮点数 x和 int 类型的整数 n,求 x 的 n 次方。
## 解题思路
-下面的讨论中 x 代表 base,n 代表 exponent。
+
-
+最直观的解法是将 x 重复乘 n 次,x\*x\*x...\*x,那么时间复杂度为 O(N)。因为乘法是可交换的,所以可以将上述操作拆开成两半 (x\*x..\*x)\* (x\*x..\*x),两半的计算是一样的,因此只需要计算一次。而且对于新拆开的计算,又可以继续拆开。这就是分治思想,将原问题的规模拆成多个规模较小的子问题,最后子问题的解合并起来。
-
+本题中子问题是 xn/2,在将子问题合并时将子问题的解乘于自身相乘即可。但如果 n 不为偶数,那么拆成两半还会剩下一个 x,在将子问题合并时还需要需要多乘于一个 x。
+
+
+
+
因为 (x\*x)n/2 可以通过递归求解,并且每次递归 n 都减小一半,因此整个算法的时间复杂度为 O(logN)。
```java
-public double Power(double base, int exponent) {
- if (exponent == 0)
- return 1;
- if (exponent == 1)
- return base;
+public double Power(double x, int n) {
boolean isNegative = false;
- if (exponent < 0) {
- exponent = -exponent;
+ if (n < 0) {
+ n = -n;
isNegative = true;
}
- double pow = Power(base * base, exponent / 2);
- if (exponent % 2 != 0)
- pow = pow * base;
- return isNegative ? 1 / pow : pow;
+ double res = pow(x, n);
+ return isNegative ? 1 / res : res;
+}
+
+private double pow(double x, int n) {
+ if (n == 0) return 1;
+ if (n == 1) return x;
+ double res = pow(x, n / 2);
+ res = res * res;
+ if (n % 2 != 0) res *= x;
+ return res;
}
```
@@ -40,4 +49,5 @@ public double Power(double base, int exponent) {
+
diff --git a/notes/pics/image-20201105012506187.png b/notes/pics/image-20201105012506187.png
new file mode 100644
index 00000000..98e193dd
Binary files /dev/null and b/notes/pics/image-20201105012506187.png differ